扇形的面积计算公式

扇形是圆周上的一段弧所对应的区域，它由弧度正的顶点以及周围的两条半径组成。扇形是常见的一种图形，在数学、物理、建筑等各个领域都有着广泛的应用。在计算扇形面积时，我们需要用到扇形的面积计算公式。

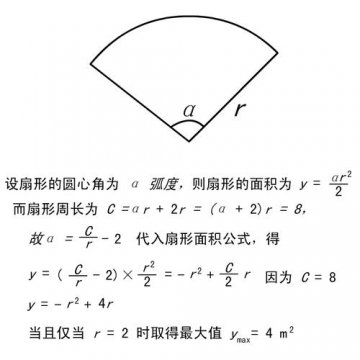
扇形的面积公式如下：

$$S = \frac{1}{2}r^2\theta$$

其中，$S$ 表示扇形的面积，$r$ 表示圆的半径，$\theta$ 表示扇形的夹角，即弧度。

在求解扇形面积时，我们需要先确定扇形的圆心角大小，然后根据圆心角大小以及圆的半径计算出扇形的面积。圆心角表示圆心的两条半径所对应的夹角大小，单位为弧度。

举一个例子来说明扇形面积的计算方法。假设给定一圆的半径为 $r=5$，以及扇形的圆心角为 $60$ 度（即 $\theta = \frac{1}{3}\pi$ 弧度），那么按照上面的公式，扇形的面积可以计算如下：

$$S = \frac{1}{2}(5)^2\frac{1}{3}\pi = \frac{25}{3}\pi$$

这个半径为 $5$ 的圆的圆心角为 $60$ 度的扇形的面积为 $\frac{25}{3}\pi$。

需要注意的是，在计算扇形面积时，一定要注意将圆心角转化成弧度制。这个公式只适用于计算半径为 $r$ 的圆上的扇形面积，对于其他形状的扇形则需要使用其他的公式进行计算。

学习了扇形的面积计算公式后，我们就可以更快速地求解扇形的面积问题了。

扇形是一个圆心角度数小于等于180度的圆形区域，它和圆形一样，也具有面积的概念。计算扇形面积的公式如下：

扇形面积 = 1/2 × 半径的平方 × 圆心角弧度

其中，圆心角弧度就是圆心角的度数除以360度后所得到的弧度数。也可以用圆心角的度数与2π（弧度的圆周角）所组成的比值来计算。

例如，有一个半径为r的扇形，圆心角为θ度。（其中0 ≤ θ ≤ 180），则扇形的面积公式可以表示为：

扇形面积 = (1/2) × r2 × (θ / 180) × π

这个公式可以简单地解释为，扇形面积等于圆形面积（即πr2）乘以圆心角弧度所占的比例（即θ/360），再乘以1/2（因为扇形是圆形的一部分）。

需要注意的是，圆心角的度数必须小于等于180度。如果圆心角的度数大于180度，则可以将整个圆形减去扇形外的部分来计算扇形面积。

例如，一个半径为r的圆形被分为两个等面积的扇形，圆心角度数为240度。此时，可以计算出一个扇形的面积，然后将它乘以2来得到整个圆形的面积。

计算扇形面积的公式是很简单的，只需要知道圆的半径和圆心角的度数即可。这个公式在很多需要用到圆形或扇形面积的情境中非常有用，例如建筑设计、工程测量以及数学计算等等。