1、SSS,即边边边,三边对应相等的三角形是全等三角形;2、SAS,即边角边,两边及其夹角对应相等的三角形是全等三角形;3、ASA,即角边角,两角及其夹边对应相等的三角形全等;4、AAS,即角角边,两角及其一角的对边对应相等的三角形全等;5、RHS,即直角、斜边、边,又称HL定理(斜边、直角边),在一对直角三角形中,斜边及另一条直角边相等。
三角形全等有五种判别方法:
1、SSS,即边边边。三边对应相等的三角形是全等三角形。
2、SAS,即边角边。两边及其夹角对应相等的三角形是全等三角形。
3、ASA,即角边角。两角及其夹边对应相等的三角形全等。
4、AAS,即角角边。两角及其一角的对边对应相等的三角形全等。
5、RHS,即直角、斜边、边,又称HL定理(斜边、直角边)。在一对直角三角形中,斜边及另一条直角边相等。
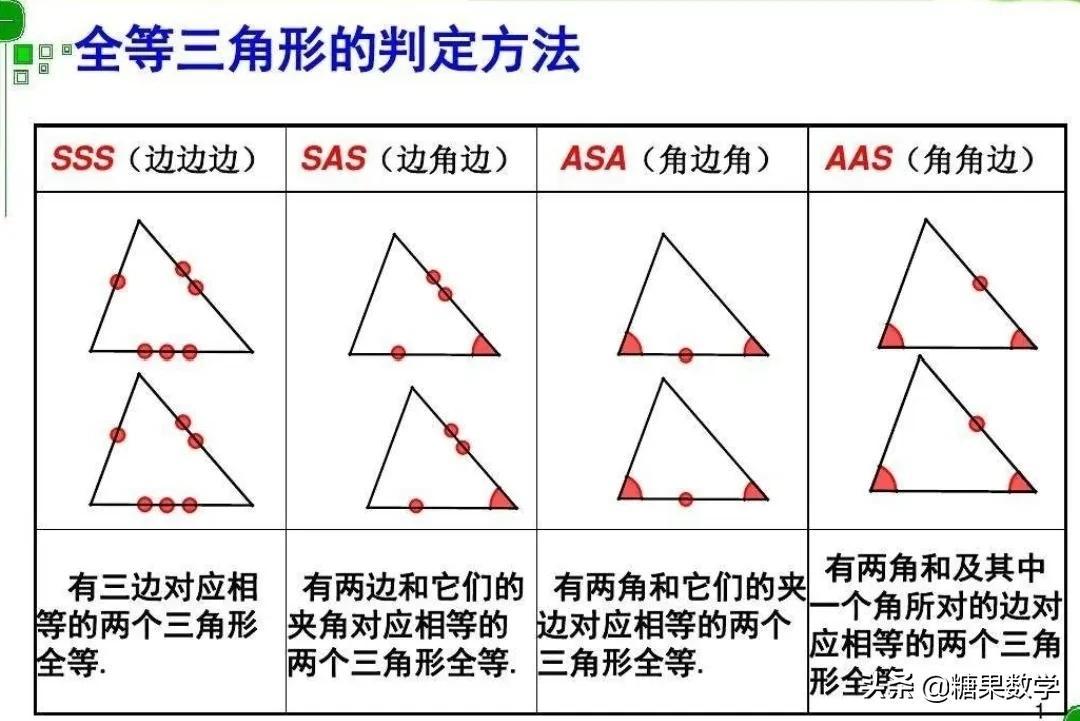
全等三角形的判定
全等三角形的性质:
1、全等三角形的对应角相等。
2、全等三角形的对应边相等。
3、能够完全重合的顶点叫对应顶点。
4、全等三角形的对应边上的高对应相等。
5、全等三角形的对应角的角平分线相
等。
6、全等三角形的对应边上的中线相等。
7、全等三角形面积和周长相等。
8、全等三角形的对应角的三角函数值相等。
全等三角形的性质
全等三角形的性质
判断三角形全等的注意:
三个角对应相等的两个三角形不一定全等,两边和其中一边的对角对应相等的两个三角形也不一定全等。
全等三角形的运用:
1、性质中三角形全等是条件,结论是对应角、对应边相等。在写两个三角形全等时,一定把对应的顶点,角、边的顺序写一致,为找对应边,角提供方便。
2、当图中出现两个以上等边三角形时。应首先考虑用SAS找全等三角形。



